Hằng số Planck – Wikipedia tiếng Việt

Hằng số Planck
Ký hiệu thường gặp	h, hoặc ħ Bạn đang đọc: Hằng số Planck – Wikipedia tiếng Việt cho hằng số Planck rút gọn
Thứ nguyên	M L 2 T − 1 { \ displaystyle { \ mathsf { M } } { \ mathsf { L } } ^ { 2 } { \ mathsf { T } } ^ { – 1 } }

Hằng số Planck là một hằng số vật lý cơ bản, ký hiệu bằng

h

{\displaystyle h}

, có tầm quan trọng to lớn trong cơ học lượng tử. Năng lượng của một photon bằng tần số của nó nhân với hằng số Planck. Do tương đương khối lượng–năng lượng, hằng số Planck cũng liên hệ giữa khối lượng và tần số.

Trong đo lường học, hằng số Planck, cùng những hằng số khác, được dùng để định nghĩa kilogram, một đơn vị SI.[1] Các đơn vị SI được định nghĩa sao cho khi biểu diễn hằng số Planck trong các đơn vị SI, nó có giá trị đúng bằng h = 6,62607015×10−34 J⋅Hz−1[2][3]

Cuối thế kỷ 19, phổ bức xạ vật đen đã được đo với độ chính xác cao, nhưng phân bố của những phép đo ở tần số cao chênh lệch đáng kể so với những tiên đoán bằng lý thuyết thời bấy giờ. Năm 1900, Max Planck bằng thực nghiệm đưa ra một công thức cho phổ quan sát được. Ông giả sử một hạt tích điện dao động trong một khoảng trống với bức xạ vật đen chỉ có thể thay đổi mức năng lượng của nó theo bước nhỏ E tỷ lệ thuận với tần số của sóng điện từ tương ứng.[4] Bằng kết quả thí nghiệm, ông tính được hằng số tỷ lệ này, và hằng số đó được đặt tên để vinh danh ông. Năm 1905, Albert Einstein xác định mức năng lượng tối thiểu, hay “lượng tử”, của một sóng điện từ. Lượng tử ánh sáng có tính chất giống như một hạt không mang điện, và cuối cùng có tên gọi photon. Max Planck nhận Giải Nobel Vật lý năm 1918 cho “những đóng góp của ông cho sự tiến bộ của Vật lý với phát hiện lượng tử năng lượng của ông”.

h, dạy ở đây từ 1889 đến 1928.”Bảng đồng tại Đại học Humboldt Berlin : ” Max Planck, người phát hiện lượng tử cơ bản, dạy ở đây từ 1889 đến 1928. “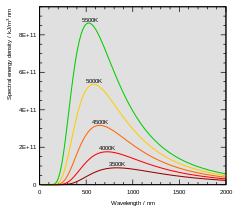 Cường độ ánh sáng phát ra từ một vật đen. Mỗi đường cong biểu diễn hành vi tại một nhiệt độ khác nhau. Hằng số Planck được dùng để lý giải hình dáng của những đường này . 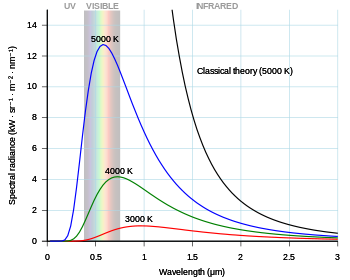The divergence of the theoretical Rayleigh – Jeans ( black ) curve from the observed Planck curves at different temperatures .Hằng số Planck xuất phát từ nỗ lực của Max Planck để đưa ra một biểu thức toán học nhằm mục đích tiên đoán phổ bức xạ từ một nguồn nhiệt kín, hay bức xạ vật đen. [ 8 ] Kết quả là một biểu thức toán học với tên gọi định luật Planck .Cuối thế kỷ 19, Max Planck xem xét yếu tố bức xạ vật đen do Kirchhoff đưa ra khoảng chừng 40 năm trước đó. Tất cả vật thể vật lý phát ra bức xạ điện từ tự động hóa và liên tục. Không có biểu thức hay lời lý giải nào cho hình dạng của phổ bức xạ quan sát được. Vào lúc đó, định luật Wien khớp với tài liệu ở bước sóng ngắn và nhiệt độ cao, nhưng sai khác trọn vẹn ở bước sóng dài. [ 8 ] : 141 Cũng vào thời gian này, Lord Rayleigh tìm ra một công thức, thời nay gọi là định luật Rayleigh – Jeans, hoàn toàn có thể tiên đoán bước sóng dài tương đối đúng chuẩn, nhưng lại không hề lý giải cho bước sóng ngắn .Planck tiếp cận yếu tố với giải thuyết rằng phương trình hoạt động của ánh sáng miêu tả một tập hợp những giao động điều hòa, mỗi tần số tương ứng với một xê dịch. Ông xem xét sự biến hóa entropy của những hạt giao động so với nhiệt độ của vật thể, làm cho nó khớp với định luật Wien, và sau cuối đưa ra một hàm số để xê dịch phổ vật đen, [ 4 ] dẫn đến một công thức thực nghiệm cho bước sóng dài .

Planck tìm ra một biểu thức khớp với định luật Wien ở bước sóng ngắn và công thức thực nghiệm ở bước sóng dài. Biểu thức này có một hằng số h, được cho là lấy từ Hilfsgrösse (biến phụ),[9] và sau được biết đến là hằng số Planck. Biểu thức cho độ rọi phổ chiếu xạ của một vật đen với tần số ν tại nhiệt độ tuyệt đối T là

B ν ( ν, T ) = 2 h ν 3 c 2 1 e h ν k B T − 1 { \ displaystyle B_ { \ nu } ( \ nu, T ) = { \ frac { 2 h \ nu ^ { 3 } } { c ^ { 2 } } } { \ frac { 1 } { e ^ { \ frac { h \ nu } { k_ { \ mathrm { B } } T } } – 1 } } }

trong đó kB là hằng số Boltzmann, h là hằng số Planck, và c là tốc độ ánh sáng trong môi trường, có thể là vật liệu hoặc chân không.[10][11][12]

Độ rọi phổ chiếu xạ (tiếng Anh: “spectral radiance”) Bν của một vật miêu tả mức năng lượng nó phát ra ở những tần số bức xạ khác nhau. Đại lượng này bằng công suất phát xạ trên một đơn vị diện tích bề mặt, trên một đơn vị góc khối, trên một đơn vị tần số. Độ rọi phổ chiếu xạ cũng có thể được biểu diễn trên một đơn vị bước sóng λ thay vì một đơn vị tần số. Trong trường hợp đó, công thức trên trở thành

B λ ( λ, T ) = 2 h c 2 λ 5 1 e h c λ k B T − 1, { \ displaystyle B_ { \ lambda } ( \ lambda, T ) = { \ frac { 2 hc ^ { 2 } } { \ lambda ^ { 5 } } } { \ frac { 1 } { e ^ { \ frac { hc } { \ lambda k_ { \ mathrm { B } } T } } – 1 } }, }

cho thấy nguồn năng lượng bức xạ ở bước sóng ngắn tăng theo nhiệt độ nhanh hơn so với ở bước sóng dài. [ 13 ]

Định luật Planck cũng có thể được biểu diễn theo những đại lượng khác, ví dụ như số photon bức xạ ở bước sóng nhất định, hay là mật độ năng lượng trên một thể tích bức xạ. Đơn vị SI của Bν là W·sr−1·m−2·Hz−1, còn của Bλ là W·sr−1·m−3.

Planck sớm nhận ra rằng giải thuật của ông không phải là duy nhất. Một số giải thuật khác sống sót, mỗi cái cho giá trị entropy của những hạt xê dịch khác nhau. [ 4 ] Để xử lý yếu tố này, Planck dùng đến cơ học thống kê, một ngành còn gây tranh cãi thời bấy giờ, [ 4 ] việc mà ông miêu tả là ” một hành vi vô vọng … tôi đã sẵn sàng chuẩn bị từ bỏ toàn bộ những niềm tin của mình trong vật lý. ” [ 14 ] Một trong những điều kiện kèm theo của giải thuật này là

coi UN [năng lượng dao động của N hạt] không phải như một đại lượng liên tục, có thể chia nhỏ tùy ý, mà như một đại lượng rời rạc gồm một số nguyên lần những phần tử hữu hạn. Ta gọi mỗi phần năng lượng như thế ε;

[4]— Planck, On the Law of Distribution of Energy in the Normal Spectrum

Với điều kiện kèm theo mới này, Planck đã lượng tử hóa nguồn năng lượng của những hạt giao động, ” một giả thuyết trọn vẹn hình thức … trong thực tiễn tôi không nghĩ nhiều về nó … ” theo lời của chính ông. [ 15 ] Áp dụng điều kiện kèm theo này cho định luật Wien cho thấy ” thành phần nguồn năng lượng ” phải tỉ lệ với tần số của giao động, ngày này gọi là ” liên hệ Planck – Einstein ” :

E = h f. { \ displaystyle E = hf. }

Sử dụng dữ liệu bức xạ vật đen từ thí nghiệm, Planck tính được giá trị của h bằng khoảng 655×10−34 J⋅s, sai khác 1,2% so với giá trị chính thức ngày nay.[4] Ông cũng là người đầu tiên xác định giá trị của hằng số Boltzmann kB bằng công thức này.[16]

Phát triển và ứng dụng[sửa|sửa mã nguồn]

Vấn đề vật đen được xét lại vào năm 1905, khi Rayleigh cùng với Jeans và độc lập với Einstein chứng minh rằng điện từ học cổ điện không thể giải thích phổ bức xạ đo được. Những chứng minh này thường được biết đến với tên gọi “thảm họa cực tím”, do Paul Ehrenfest đặt năm 1911. Chúng, cùng với nghiên cứu của Einstein về hiệu ứng quang điện, khiến các nhà vật lý học ngày càng tin rằng việc lượng tử hóa mức năng lượng của Planck có ý nghĩa sâu hơn là một công cụ toán học đơn thuần. hội nghị Solvay đầu tiên năm 1911 có chủ đề “lý thuyết bức xạ và lượng tử”.[17]

Hiệu ứng quang điện[sửa|sửa mã nguồn]

Hiệu ứng quang điện là sự phát xạ electron ( gọi là ” quang điện tử ” ) từ một mặt phẳng có ánh sáng chiếu vào. Hiện tượng này lần đầu được quan sát bởi Alexandre Edmond Becquerel năm 1839, mặc dầu những nguồn thường ghi nhận Heinrich Hertz, [ 18 ] người xuất bản điều tra và nghiên cứu chi tiết cụ thể tiên phong năm 1887. Một nghiên cứu và điều tra khác của Philipp Lenard ( Lénárd Fülöp ) được xuất bản năm 1902. [ 19 ] Năm 1905, Einstein viết bài báo [ 20 ] bàn luận về hiện tượng kỳ lạ này bằng lượng tử ánh sáng, một thành tựu đã cho ông giải Nobel Vật lý năm 1921, [ 18 ] sau khi những tiên đoán của ông được xác nhận bởi Robert Andrews Millikan. [ 21 ]Trước bài báo của Einstein, bức xạ điện từ như ánh sáng được coi là có hành vi của sóng : đó cũng là nguồn gốc cho những thuật ngữ ” tần số ” và ” bước sóng ” dùng để miêu tả những loại bức xạ khác nhau. Năng lượng của một sóng trên một đơn vị chức năng thời hạn là cường độ. Ánh sáng từ một đèn pha sân khấu có cường độ lớn hơn ánh sáng của một bóng đèn gia dụng, tức đèn pha tỏa ra nhiều nguồn năng lượng hơn trên một đơn vị chức năng thời hạn và một đơn vị chức năng khoảng trống, ngay cả khi sắc tố của hai bóng đèn rất giống nhau. Những loại sóng khác như âm thanh hay sóng biển cũng có cường độ của chúng. Tuy nhiên, nguồn năng lượng của hiệu ứng quang điện không có đặc thù giống như sóng ánh sáng .

Các quang điện tử được phát ra có động năng nhất định, và động năng của mỗi quang điện tử là độc lập với cường độ của ánh sáng,[19] nhưng tỷ lệ thuận với tần số,[21] và nếu tần số quá thấp, sẽ không có quang điện tử nào được phát ra.[22] Giả sử tần số đủ cao để gây ra hiệu ứng quang điện, cường độ nguồn sáng tăng dẫn đến nhiều quang điện tử với cùng động năng được phát ra, thay vì cùng số lượng quang điện tử với động năng lớn hơn.[19]

Einstein lý giải những quan sát này với việc lượng tử hóa ánh sáng : nguồn năng lượng ánh sáng không được truyền liên tục dưới dạng sóng, mà chỉ theo những ” gói ” nhỏ hay lượng tử. Những ” gói ” nguồn năng lượng này, về sau được gọi là photon, có độ lớn bằng những ” thành phần nguồn năng lượng ” của Planck, dẫn đến liên hệ Planck – Einstein :

E = h f. { \ displaystyle E = hf. }

Giả thiết của Einstein về sau được chứng tỏ bằng thực nghiệm : hằng số tỉ lệ giữa tần số nguồn sáng f và động năng của những quang điện tử E bằng với hằng số Planck h. [ 21 ]

Cấu trúc nguyên tử[sửa|sửa mã nguồn]

n = 3

lên

n = 2

phát ra ánh sáng với bước sóng 656 nm (đỏ), đúng như dự đoán.Giản đồ quy mô Bohr cho nguyên tử hydro. Mức chuyển từlênphát ra ánh sáng với bước sóng 656 nm ( đỏ ), đúng như Dự kiến .

Năm 1912, John William Nicholson giới thiệu h-bar vào lý thuyết nguyên tử và là người đầu tiên lượng tử hóa tần số góc thành h/2π. [23][24][25] Niels Bohr trích dẫn ông trong bài báo mô hình nguyên tử Bohr năm 1913.[26] Ảnh hưởng của mô hình hạt nhân nguyên tử Nicholson lên mô hình của Bohr đã được nhiều nhà sử học nghiên cứu.[27][28][29]

Năm 1913, Niels Bohr đưa ra mô hình lượng tử của nguyên tử thứ ba, nhằm giải quyết những thiếu sót của mô hình Rutherford cổ điển. Mô hình nguyên tử lượng tử đầu tiên được đề xuất bởi Arthur Erich Haas năm 1910 và được thảo luận chi tiết ở Hội nghị Solvay 1911.[30][31] Trong điện từ học cổ điển, một điện tích chuyển động tròn sẽ phát ra bức xạ điện từ. Nếu điện tích đó là một electron quay quanh hạt nhân, bức xạ sẽ khiến nó mất năng lượng và rơi dần vào hạt nhân. Bohr giải quyết nghịch lý này với cảm hứng từ công trình của Planck: một electron trong nguyên tử Bohr chỉ có thể có mức năng lượng định trước En, trong đó

E n = − h c R ∞ n 2, { \ displaystyle E_ { n } = – { \ frac { hcR_ { \ infty } } { n ^ { 2 } } }, }

với c là tốc độ ánh sáng trong chân không, R∞ là hằng số xác định từ thực nghiệm (hằng số Rydberg), và n ∈ {1, 2, 3, …}. Khi electron đạt mức năng lượng thấp nhất (n = 1), nó không thể tiến gần hơn đến hạt nhân nữa. Phương pháp này cho phép Bohr tính đến công thức Rydberg, một miêu tả thực nghiệm cho phổ nguyên tử của hydro, và giải thích cho giá trị của hằng số Rydberg R∞ bằng những hằng số cơ bản khác.

Bohr cũng đề xuất đại lượng ħ = h / (2π), ngày nay gọi là hằng số Planck rút gọn, làm lượng tử cho mô men động lượng. Ban đầu, Bohr cho rằng đại lượng này là mômen động lượng của mỗi electron trong nguyên tử, nhưng giả thiết này sai, và mặc cho nỗ lực của Arnold Sommerfeld và những người khác, mô hình Bohr không thể miêu tả chính xác mômen động lượng của electron. Quy luật lượng tử hóa tổng quát cho electron – trong đó mô hình Bohr là trường hợp đặc biệt cho nguyên tử hydro – được miêu tả bởi cơ học ma trận của Heisenberg năm 1925 và phương trình sóng Schrödinger năm 1926, và hằng số Planck rút gọn vẫn là lượng tử cơ bản cho mômen động lượng. Cụ thể hơn, nếu J là tổng mômen động lượng của một hệ với bất biến quay và Jz là mômen động lượng đối với một trục bất kỳ, chúng chỉ có thể mang các giá trị

J 2 = j ( j + 1 ) ℏ 2, j = 0 2, 1 2, 2 2, 3 2, …, J z = m ℏ, m = − j, − j + 1, …, j. { \ displaystyle { \ begin { aligned } J ^ { 2 } = j ( j + 1 ) \ hbar ^ { 2 }, \ qquad và j = { \ frac { 0 } { 2 } }, { \ frac { 1 } { 2 } }, { \ frac { 2 } { 2 } }, { \ frac { 3 } { 2 } }, \ ldots, \ \ J_ { z } = m \ hbar, \ qquad \ qquad \ quad và m = – j, – j + 1, \ ldots, j. \ end { aligned } } }

Nguyên lý bất định[sửa|sửa mã nguồn]

Hằng số Planck cũng xuất hiện trong biểu thức của nguyên lý bất định của Werner Heisenberg. Với nhiều hạt ở cùng trạng thái, sự bất định về vị trí Δx và sự bất định về động lượng Δpx thỏa mãn

Δ x Δ p x ≥ ℏ 2, { \ displaystyle \ Delta x \, \ Delta p_ { x } \ geq { \ frac { \ hbar } { 2 } }, }

trong đó sự bất định được định nghĩa là độ lệch chuẩn của giá trị đo được từ giá trị kỳ vọng. Có 1 số ít cặp biến phối hợp đo được khác tuân theo một nguyên tắc tựa như, ví dụ như thời hạn và nguồn năng lượng. Mối quan hệ tỉ lệ nghịch giữa hai độ bất định này dẫn đến một đánh đổi trong những thí nghiệm lượng tử, khi mà càng đo đúng chuẩn một đại lượng khiến đại lượng kia càng rơi lệch .

Ngoài ra, một trong những nền móng của cơ học lượng tử nằm trong quan hệ giao hoán tử giữa toán tử vị trí

x
^

{\displaystyle {\hat {x}}}

và toán tử động lượng

p
^

{\displaystyle {\hat {p}}}

:

[ p ^ i, x ^ j ] = − i ℏ δ i j, { \ displaystyle [ { \ hat { p } } _ { i }, { \ hat { x } } _ { j } ] = – i \ hbar \ delta _ { ij }, }

trong đó δij là Kronecker delta.

Hằng số Planck có thứ nguyên của mômen động lượng. Trong đơn vị SI, hằng số Planck được biểu diễn bằng joule trên hertz (J⋅Hz−1 hoặc kg⋅m2⋅s−1). Một điểm cần lưu ý trong thứ nguyên của hằng số Planck là việc đơn vị SI của tần số, hertz, biểu diễn một chu kỳ trọn vẹn, 360 độ hay 2π radian, một giây. Tần số góc bằng radian trên giây thường tự nhiên hơn trong toán và vật lý, và nhiều công thức sử dụng hằng số Planck rút gọn.[note 1]

h = 6.626 070 15 × 10 − 34 J ⋅ Hz − 1 { \ displaystyle h = 6.626 \ 070 \ 15 \ times 10 ^ { – 34 } \ { \ text { J } } { \ cdot } { \ text { Hz } } ^ { – 1 } }

ℏ = h 2 π = 1.054 571 817 … × 10 − 34 J ⋅ s = 6.582 119 569 … × 10 − 16 eV ⋅ s { \ displaystyle \ hbar = { { h } \ over { 2 \ pi } } = 1.054 \ 571 \ 817 … \ times 10 ^ { – 34 } \ { \ text { J } } { \ cdot } { \ text { s } } = 6.582 \ 119 \ 569 … \ times 10 ^ { – 16 } \ { \ text { eV } } { \ cdot } { \ text { s } } }

Các giá trị trên là chính xác và cố định theo sau lần định nghĩa lại đơn vị cơ bản SI năm 2019.

1. ^ ħ còn được gọi là “hằng số Dirac”, theo tên [32]Đôi khicòn được gọi là ” hằng số Dirac “, theo tên Paul Dirac

Liên kết ngoài[sửa|sửa mã nguồn]

Source: https://thevesta.vn
Category: Bản Tin