Công thức tính khoảng cách từ một điểm đến một đường thẳng và bài tập áp dụng – https://thevesta.vn
I. PHƯƠNG PHÁP
Cho điểm ${M_0}\left( {{x_0};{y_0};{z_0}} \right)$ và đường thẳng $\Delta :\left\{ {\begin{array}{*{20}{l}}
{x = x’ + {u_1}t}\\
{y = y’ + {u_2}t}\\
{z = z’ + {u_3}t}
\end{array}} \right.$ $(t \in R).$
Cách 1:
+ Bước 1: Xác định một vectơ chỉ phương $\vec u\left( {{u_1};{u_2};{u_3}} \right)$ và một điểm $M\left( {{x_M};{y_M};{z_M}} \right) \in \Delta .$
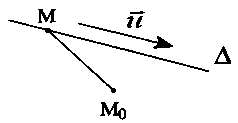
Bạn đang đọc: Công thức tính khoảng cách từ một điểm đến một đường thẳng và bài tập áp dụng – https://thevesta.vn
+ Bước 2 : Lúc đó : USD d \ left ( { { M_0 } ; \ Delta } \ right ) = \ frac { { \ left | { \ left [ { \ vec u, \ overrightarrow { { M_0 } M } } \ right ] } \ right | } } { { | \ vec u | } }. $
Cách 2:
+ Bước 1: Gọi $H$ là hình chiếu vuông góc của ${M_0}$ trên $\Delta $ (toạ độ $H$ phụ thuộc một ẩn $t$).

+ Bước 2: Xác định $H$ dựa vào: $\overrightarrow {{M_0}H} .\vec u = 0.$
$ \Rightarrow d\left( {{M_0};\Delta } \right) = {M_0}H.$
Nhận xét: Nếu giải quyết bài toán theo cách 2 thì khoa học và đảm bảo được nhiều yêu cầu như: xác định hình chiếu, viết phương trình đường thẳng vuông góc ….
Hệ quả:
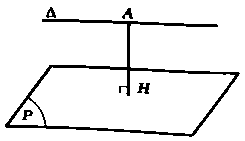
+ Khoảng cách giữa hai đường thẳng song song: Cho hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ song song với nhau. Lúc đó: $d\left( {{\Delta _1};{\Delta _2}} \right) = d\left( {A;{\Delta _2}} \right)$ với $A \in {\Delta _1}.$

+ Khoảng cách giữa đường thẳng và mặt phẳng song song : Cho đường thẳng $ \ Delta $ và mặt phẳng USD ( P. ) USD song song với nhau. Lúc đó : USD d ( \ Delta ; ( P. ) ) = d ( A ; ( P. ) ) USD với $ A \ in \ Delta. $
II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Ví dụ 1: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ điểm $A(1;1;1)$ đến đường thẳng $\Delta :\frac{x}{1} = \frac{{y – 1}}{2} = \frac{{z + 1}}{1}.$
A. $d = \frac{{\sqrt {14} }}{2}.$
B. $d = \frac{{3\sqrt 3 }}{2}.$
C. $d = \sqrt {14} .$
D. $d = 3\sqrt 3 .$
Lời giải:
+ Cách 1: Xác định hình chiếu vuông góc của $A$ trên $\Delta .$
Đường thẳng $\Delta $ có một vectơ chỉ phương là ${\vec u_\Delta } = (1;2;1).$
Ta có: $\Delta :\left\{ {\begin{array}{*{20}{l}}
{x = t}\\
{y = 1 + 2t}\\
{z = – 1 + t}
\end{array}} \right..$ Gọi ${H(t;1 + 2t; – 1 + t) \in \Delta }$, $H$ là hình chiếu vuông góc của $A$ trên $\Delta $ $ \Leftrightarrow \overrightarrow {AH} .{\vec u_\Delta } = 0$ $ \Leftrightarrow 6t – 3 = 0$ $ \Leftrightarrow t = \frac{1}{2}$ $ \Rightarrow H\left( {\frac{1}{2};1; – \frac{1}{2}} \right).$ Vậy $d = AH = \frac{{\sqrt {14} }}{2}.$
+ Cách 2: Sử dụng công thức.
Đường thẳng $\Delta $ có một vectơ chỉ phương là ${\vec u_\Delta } = (1;2;1).$
Chọn $B(0;1; – 1) \in \Delta $ $ \Rightarrow \overrightarrow {AB} = ( – 1;0; – 2)$ $ \Rightarrow [\overrightarrow {AB} ,\vec u] = (4; – 1; – 2).$
Lúc đó: $d = \frac{{\left| {\left[ {\overrightarrow {AB} ,\vec u} \right]} \right|}}{{|\vec u|}} = \frac{{\sqrt {14} }}{2}.$
Chọn đáp án A.
Ví dụ 2: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;1;1)$ và đường thẳng $\Delta :\frac{x}{1} = \frac{{y – 1}}{2} = \frac{{z + 1}}{1}.$ Gọi $M$ là điểm bất kì trên $\Delta $, tìm giá trị nhỏ nhất của độ dài đoạn thẳng $AM.$
A. $\frac{{\sqrt {14} }}{4}.$
B. $\frac{{\sqrt {14} }}{2}.$
C. $\sqrt {14} .$
D. $3\sqrt 3 .$
Lời giải:
Ta có: $A{M_{\min }} = d(A;\Delta ).$
Đường thẳng $\Delta $ có một vectơ chỉ phương là ${\vec u_\Delta } = (1;2;1).$
Chọn $B(0;1; – 1) \in \Delta $ $ \Rightarrow \overrightarrow {AB} = ( – 1;0; – 2)$ $ \Rightarrow [\overrightarrow {AB} ,\vec u] = (4; – 1; – 2).$
Lúc đó: $d(A;\Delta ) = \frac{{\left| {\left[ {\overrightarrow {AB} ,\overrightarrow u } \right]} \right|}}{{|\vec u|}} = \frac{{\sqrt {14} }}{2}$ $ \Rightarrow A{M_{\min }} = \frac{{\sqrt {14} }}{2}.$
Chọn đáp án B.
Ví dụ 3: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1;1;1)$, $B(0;1;-1)$ và đường thẳng $\Delta :\frac{x}{1} = \frac{{y – 1}}{2} = \frac{{z + 1}}{1}.$ Gọi $H$ là hình chiếu vuông góc của $A$ trên $\Delta $, tính diện tích $S$ của tam giác $AHB.$
A. $S = \frac{{\sqrt {21} }}{2}.$
B. $S = \sqrt 6 .$
C. $S = \frac{{\sqrt {21} }}{4}.$
D. $S = 3\sqrt 3 .$
Lời giải:
Đường thẳng $\Delta $ có một vectơ chỉ phương là ${\vec u_\Delta } = (1;2;1).$
Chọn $K(2;5;1) \in \Delta $ $ \Rightarrow \overrightarrow {AK} = (1;4;0)$ $ \Rightarrow [\overrightarrow {AK} ,\vec u] = (4; – 1; – 2).$
Lúc đó: $d(A;\Delta ) = \frac{{\left| {\left[ {\overrightarrow {AK} ,\vec u} \right]} \right|}}{{|\vec u|}} = \frac{{\sqrt {14} }}{2}$ $ \Rightarrow AH = \frac{{\sqrt {14} }}{2}.$
Để ý rằng $B \in \Delta $ $ \Rightarrow \Delta ABH$ vuông tại $H$ $ \Rightarrow HB = \sqrt {A{B^2} – A{H^2}} = \frac{{\sqrt 6 }}{2}.$
Vậy $S = \frac{1}{2}AH.HB = \frac{{\sqrt {21} }}{4}.$
Chọn đáp án C.
Ví dụ 4: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;0;2)$ và đường thẳng $\Delta :\frac{x}{1} = \frac{{y – m}}{2} = \frac{{z + 1}}{2}$, $m$ là tham số thực. Có bao nhiêu giá trị nguyên của tham số $m$ để khoảng cách từ $A$ đến $\Delta $ bằng $\sqrt 2 $?
A. $2.$
B. $0.$
C. $1.$
D. Vô số.
Lời giải:
Đường thẳng $\Delta $ có một vectơ chỉ phương là ${\vec u_\Delta } = (1;2;2).$
Chọn $B(0;m; – 1) \in \Delta $ $ \Rightarrow \overrightarrow {AB} = ( – 1;m; – 3)$ $ \Rightarrow [\overrightarrow {AB} ,\vec u] = (2m + 6; – 1; – 2 – m).$
Lúc đó: $d = \frac{{\left| {\left[ {\overrightarrow {AB} ,\vec u} \right]} \right|}}{{|\vec u|}}$ $ = \frac{{\sqrt {5{m^2} + 28m + 41} }}{3} = \sqrt 2 .$
$ \Leftrightarrow 5{m^2} + 28m + 23 = 0$ $ \Leftrightarrow m = – 1 \vee m = – \frac{{23}}{5}.$
Chọn đáp án C.
Xem thêm: Nhạc tiền chiến – Wikipedia tiếng Việt
Ví dụ 5: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $P(1;2;3)$, $Q(1;0;-1)$ và đường thẳng $\Delta :\frac{x}{1} = \frac{{y – 1}}{2} = \frac{{z + 1}}{1}.$ Gọi $M$ là điểm bất kì trên $\Delta $, tìm độ dài nhỏ nhất của vectơ $\overrightarrow {MP} + \overrightarrow {MQ} .$
A. $\frac{{\sqrt {14} }}{2}.$
B. $\frac{{3\sqrt 3 }}{2}.$
C. $\sqrt {14} .$
D. $2\sqrt 3 .$
Lời giải:
Ta có: $\overrightarrow {MP} + \overrightarrow {MQ} = 2\overrightarrow {MI} $ $ \Rightarrow |\overrightarrow {MP} + \overrightarrow {MQ} {|_{\min }}$ $ = 2M{I_{\min }} = 2d(I;\Delta ).$
Ta có: $I(1;1;1).$ Đường thẳng $\Delta $ có một vectơ chỉ phương là ${\vec u_\Delta } = (1;2;1).$
Chọn $B(0;1; – 1) \in \Delta $ $ \Rightarrow \overrightarrow {IB} = ( – 1;0; – 2)$ $ \Rightarrow [\overrightarrow {IB} ,\vec u] = (4; – 1; – 2).$
Lúc đó: $d = \frac{{\left| {\left[ {\overrightarrow {IB} ,\vec u} \right]} \right|}}{{|\vec u|}} = \frac{{\sqrt {14} }}{2}$ $ \Rightarrow |\overrightarrow {MP} + \overrightarrow {MQ} {|_{\min }} = \sqrt {14} .$
Chọn đáp án C.
Ví dụ 6: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng ${\Delta _1}:\frac{{x – 1}}{2} = \frac{{y – 1}}{4} = \frac{{z – 1}}{2}$ và ${\Delta _2}:\frac{x}{1} = \frac{{y – 1}}{2} = \frac{{z + 1}}{1}.$ Tính khoảng cách $d$ giữa ${\Delta _1}$ và ${\Delta _2}.$
A. $\frac{{\sqrt {14} }}{4}.$
B. $\frac{{\sqrt {14} }}{2}.$
C. $\sqrt {14} .$
D. $3\sqrt 3 .$
Lời giải:
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = (2;4;2).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (1;2;1).$
Chọn $A(1;1;1) \in {\Delta _1}$, ta có: $\left\{ {\begin{array}{*{20}{l}}
{{{\vec u}_1} = 2{{\vec u}_2}}\\
{A \in {\Delta _2}}
\end{array}} \right.$ $ \Rightarrow {\Delta _1}//{\Delta _2}$ $ \Rightarrow d\left( {{\Delta _1};{\Delta _2}} \right) = d\left( {A;{\Delta _2}} \right).$
Chọn $B(0;1; – 1) \in {\Delta _2}$ $ \Rightarrow \overrightarrow {AB} = ( – 1;0; – 2)$ $ \Rightarrow \left[ {\overrightarrow {AB} ,{{\vec u}_2}} \right] = (4; – 1; – 2).$
Lúc đó: $d\left( {A;{\Delta _2}} \right) = \frac{{\left| {\left[ {\overrightarrow {AB} ,{{\vec u}_2}} \right]} \right|}}{{\left| {{{\vec u}_2}} \right|}} = \frac{{\sqrt {14} }}{2}$ $ \Rightarrow d = \frac{{\sqrt {14} }}{2}.$
Chọn đáp án B.
Ví dụ 7: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $K(1;1;1)$ và đường thẳng $\Delta :\frac{x}{1} = \frac{{y – 1}}{2} = \frac{{z + 1}}{1}.$ Viết phương trình mặt cầu tâm $K$ và tiếp xúc với $\Delta .$
A. ${(x – 1)^2} + {(y – 1)^2} + {(z – 1)^2} = \frac{7}{2}.$
B. ${(x – 1)^2} + {(y – 1)^2} + {(z – 1)^2} = 7.$
C. ${(x – 1)^2} + {(y – 1)^2} + {(z – 1)^2} = 14.$
D. ${(x – 1)^2} + {(y – 1)^2} + {(z – 1)^2} = 8.$
Lời giải:
Mặt cầu $(S)$ tâm $K$ và tiếp xúc với $\Delta $ nên có bán kính $R = d(K;\Delta ).$
Đường thẳng $\Delta $ có một vectơ chỉ phương là $\vec u = (1;2;1).$
Chọn $B(0;1; – 1) \in \Delta $ $ \Rightarrow \overrightarrow {KB} = ( – 1;0; – 2)$ $ \Rightarrow [\overrightarrow {KB} ,\vec u] = (4; – 1; – 2).$
Lúc đó: $d(K;\Delta ) = \frac{{\left| {\left[ {\overrightarrow {KB} ,\vec u} \right]} \right|}}{{|\vec u|}} = \frac{{\sqrt {14} }}{2}$ $ \Rightarrow R = \frac{{\sqrt {14} }}{2}.$
Vậy $(S):{(x – 1)^2} + {(y – 1)^2} + {(z – 1)^2} = \frac{7}{2}.$
Chọn đáp án B.
Ví dụ 8: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1;2;4)$ và $B(0;1;3).$ Viết phương trình mặt cầu tâm $A$ và tiếp xúc với đường thẳng $OB.$
A. ${(x – 1)^2} + {(y – 2)^2} + {(z – 4)^2} = \frac{7}{5}.$
B. ${(x – 1)^2} + {(y – 2)^2} + {(z – 4)^2} = \frac{7}{4}.$
C. ${(x – 1)^2} + {(y – 2)^2} + {(z – 4)^2} = \frac{{14}}{5}.$
D. ${(x – 1)^2} + {(y – 2)^2} + {(z – 4)^2} = \frac{7}{2}.$
Lời giải:
Mặt cầu $(S)$ tâm $A$ và tiếp xúc với $OB$ nên có bán kính $R = d(A;OB).$
$\overrightarrow {OA} = (1;2;4).$
Đường thẳng $OB$ có một vectơ chỉ phương là $\overrightarrow {OB} = (0;1;3)$ $ \Rightarrow [\overrightarrow {OB} ,\overrightarrow {OA} ] = ( – 2;3; – 1).$
Lúc đó: $d = \frac{{\left| {\left[ {\overrightarrow {OB} ,\overrightarrow {OA} } \right]} \right|}}{{|\overrightarrow {OB} |}} = \frac{{\sqrt {35} }}{5}$ $ \Rightarrow R = \frac{{\sqrt {35} }}{5}.$
Vậy $(S):{(x – 1)^2} + {(y – 2)^2} + {(z – 4)^2} = \frac{7}{5}.$
Chọn đáp án A.
III. LUYỆN TẬP
1. ĐỀ BÀI
Câu 1: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ điểm $A(1;0;1)$ đến đường thẳng $\Delta :\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z – 1}}{3}.$
A. $d = \frac{{\sqrt {266} }}{{14}}.$
B. $d = \frac{{\sqrt {226} }}{7}.$
C. $d = \frac{{3\sqrt {226} }}{{14}}.$
D. $d = \frac{{\sqrt {226} }}{{14}}.$
Câu 2: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;0;1)$ và đường thẳng $\Delta :\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z – 1}}{3}.$ $M$ là điểm bất kì trên $\Delta $, tìm giá trị nhỏ nhất của độ dài đoạn thẳng $AM.$
A. $d = \frac{{\sqrt {226} }}{7}.$
B. $d = \frac{{\sqrt {266} }}{{14}}.$
C. $d = \frac{{3\sqrt {226} }}{{14}}.$
D. $d = \frac{{\sqrt {226} }}{{14}}.$
Câu 3: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1;0;1)$, $B(2;0;4)$ và đường thẳng $\Delta :\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z – 1}}{3}.$ Gọi $H$ là hình chiếu vuông góc của $A$ trên $\Delta $, tính diện tích $S$ của tam giác $AHB.$
A. $S = \frac{{\sqrt {19} }}{{28}}.$
B. $S = \frac{{11\sqrt {19} }}{{14}}.$
C. $S = \frac{{11\sqrt {19} }}{{28}}.$
D. $S = \frac{{5\sqrt {19} }}{{28}}.$
Câu 4: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $P(2;1;3)$, $Q(0;-1;-1)$ và đường thẳng $\Delta :\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z – 1}}{3}.$ Gọi $M$ là điểm bất kì trên $\Delta $, tìm độ dài nhỏ nhất của vectơ $\overrightarrow {MP} + \overrightarrow {MQ} .$
A. $\frac{{\sqrt {266} }}{{14}}.$
B. $\frac{{2\sqrt {266} }}{7}.$
C. $\frac{{\sqrt {266} }}{7}.$
D. $\frac{{5\sqrt {266} }}{7}.$
Câu 5: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng ${\Delta _1}:\frac{{x – 1}}{{ – 2}} = \frac{y}{{ – 1}} = \frac{{z – 1}}{{ – 3}}$ và ${\Delta _2}:\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z – 1}}{3}.$ Tính khoảng cách $d$ giữa ${\Delta _1}$ và ${\Delta _2}.$
A. $d = \frac{{\sqrt {266} }}{{14}}.$
B. $d = \frac{{2\sqrt {266} }}{7}.$
C. $d = \frac{{\sqrt {266} }}{7}.$
D. $d = \frac{{5\sqrt {266} }}{7}.$
Câu 6: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $K(1;0;1)$ và đường thẳng $\Delta :\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z – 1}}{3}.$ Viết phương trình mặt cầu tâm $K$ và tiếp xúc với $\Delta .$
A. ${(x – 1)^2} + {y^2} + {(z – 1)^2} = \frac{{19}}{{14}}.$
B. ${(x – 1)^2} + {y^2} + {(z – 1)^2} = \frac{{19}}{7}.$
C. ${(x – 1)^2} + {y^2} + {(z – 1)^2} = \frac{{19}}{4}.$
D. ${(x – 1)^2} + {y^2} + {(z – 1)^2} = \frac{{19}}{3}.$
Câu 7: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1;2;4)$ và $B(0;1;3).$ Tính khoảng cách $d$ từ $A$ đến đường thẳng $OB.$
A. $d = \frac{{\sqrt {266} }}{{14}}.$
B. $d = \frac{{2\sqrt {266} }}{7}.$
C. $d = \frac{{\sqrt {266} }}{7}.$
D. $d = \frac{{5\sqrt {266} }}{7}.$
Câu 8: Trong không gian với hệ tọa độ $Oxyz$, cho tam giác $ABC$, biết $A(1;1;1)$, $B(2; – 1;3)$ và $C( – 1;4;0).$ Tính độ dài $h$ của đường cao kẻ từ $A$ của tam giác $ABC.$
A. $h = \frac{{\sqrt {1118} }}{{43}}.$
B. $h = \frac{{\sqrt {1118} }}{{23}}.$
C. $h = \frac{{2\sqrt {1118} }}{{43}}.$
D. $h = \frac{{2\sqrt {1118} }}{{23}}.$
Câu 9: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;0;2)$ và đường thẳng $\Delta :\frac{x}{1} = \frac{{y – m}}{2} = \frac{{z + 1}}{2}$, $m$ là tham số thực. Tìm tập hợp tất cả các giá trị thực của tham số $m$ để khoảng cách từ $A$ đến $\Delta $ bằng $\sqrt 2 .$
A. $\left\{ { – 1;\frac{{23}}{5}} \right\}.$
B. $\left\{ {1; – \frac{{23}}{5}} \right\}.$
C. $\left\{ { – 1; – \frac{{23}}{5}} \right\}.$
D. $\left\{ { – \frac{{23}}{5};\frac{{23}}{5}} \right\}.$
Câu 10: Trong không gian $Oxyz$, cho $A(1;3;-2)$, $B(3;5;-12).$ Đường thẳng $AB$ cắt mặt phẳng $Oyz$ tại $N.$ Tính tỉ số $\frac{{BN}}{{AN}}.$
A. $\frac{{BN}}{{AN}} = 4.$
B. $\frac{{BN}}{{AN}} = 2.$
C. $\frac{{BN}}{{AN}} = 5.$
D. $\frac{{BN}}{{AN}} = 3.$
2. BẢNG ĐÁP ÁN
| Câu | 1 | 2 | 3 | 4 | 5 |
| Đáp án | A | B | C | C | A |
| Câu | 6 | 7 | 8 | 9 | 10 |
| Đáp án | A | A | A | C | D |
Source: https://thevesta.vn
Category: Chỉ Đường





