Công thức khoảng cách từ điểm đến mặt phẳng – https://thevesta.vn

Trong hình học khoảng trống Oxyz, ta có nhiều cách để tính được khoảng cách từ điểm đến mặt phẳng. Tuy nhiên, nếu đề cho biết tọa độ 1 điểm và phương trình 1 mặt phẳng thì ta nên dùng công thức dưới đây sẽ cho hiệu quả nhanh và đúng mực .

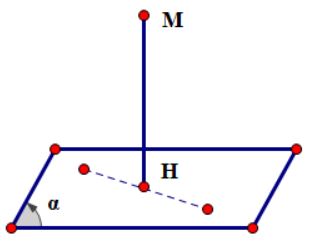
Cơ sở lý thuyết

Trong không gian Oxyz có điểm P(a; b; c) không thuộc mặt phẳng (α), biết rằng mặt phẳng này có phương trình (α): Ax + By + Cz + D = 0. Để tính khoảng cách từ điểm P(a; b; c) tới mặt phẳng (α) ta sử dụng công thức:

d ( P, ( α ) ) = $ \ frac { { \ left | { a. A + b. B + c. C + D } \ right | } } { { \ sqrt { { A ^ 2 } + { B ^ 2 } + { C ^ 2 } } } } $

Bài tập có lời giải

Bài tập 1.Trong không gian có mặt phẳng (α): x – 2y + 3z – 4 = 0. Hãy tìm khoảng cách từ P(1; 1; 1) tới mặt phẳng (α)?

Hướng dẫn giải
Áp dụng công thức tính khoảng cách ở trên : d ( P, ( α ) ) = $ \ frac { { \ left | { 1.1 + 1. \ left ( { – 2 } \ right ) + 1. \ left ( 3 \ right ) – 4 } \ right | } } { { \ sqrt { { 1 ^ 2 } + { { \ left ( { – 2 } \ right ) } ^ 2 } + { 3 ^ 2 } } } } = \ frac { { \ sqrt { 14 } } } { 7 } $
Kết luận : d ( P, ( α ) ) = $ \ frac { { \ sqrt { 14 } } } { 7 } $

Bài tập 2. Cho mặt phẳng (α): x + y + z – 9 = 0. Một điểm P nằm trên trục tọa độ Oz thuộc hệ trục Oxyz, cách (α) là 5. Hãy tìm tọa độ của M?

Hướng dẫn giải
Vì P thuộc Oz nên nó có tọa độ là P ( 0 ; 0 ; z ) .
Theo công thức khoảng cách ở trên : d ( P, ( α ) ) = 5

$5 = \frac{{\left| {1.0 + 1.0 + 1.z – 9} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} \Leftrightarrow z = 5\sqrt 3 + 9$

Kế luận : P ( 0 ; 0 ; USD 5 \ sqrt 3 + 9 USD )

Bài tập 3. Hãy tính khoảng cách từ gốc tọa độ O của hệ trục Oxyz tới mặt phẳng (Q): 2x – 3y – 5z + 2 = 0

Hướng dẫn giải
Gốc tọa độ của hệ trục Oxyz có tọa độ O ( 0 ; 0 ; 0 )
Áp dụng công thức tính khoảng cách ở trên : d ( O, ( Q. ) ) = $ \ frac { { \ left | { 2.0 + \ left ( { – 3 } \ right ). 0 + \ left ( { – 5 } \ right ). 0 + 2 } \ right | } } { { \ sqrt { { 2 ^ 2 } + { { \ left ( { – 3 } \ right ) } ^ 2 } + { { \ left ( { – 5 } \ right ) } ^ 2 } } } } = \ frac { { \ sqrt { 38 } } } { { 19 } } $

Bài tập 4. Một mặt phẳng (α): – x + 2y + 3z – 4 = 0. Biết khoảng cách từ mp (α) tới P thuộc trục Ox là 2. Hãy xác định tọa độ điểm P.

Hướng dẫn giải
Vì P thuộc Ox nên nó có tọa độ P ( x ; 0 ; 0 )
Theo đề bài : d ( P, ( α ) ) = 2

Áp dụng công thức tính khoảng cách: 2 = $\frac{{\left| {\left( { – 1} \right).x + 2.0 + 3.0 – 4} \right|}}{{\sqrt {{{\left( { – 1} \right)}^2} + {2^2} + {3^2}} }} \Leftrightarrow x = 2\sqrt {14} – 4$

Vậy P ( USD 2 \ sqrt { 14 } – 4 USD ; 0 ; 0 )
Bài viết khoảng cách từ 1 điểm đến mặt phẳng tạm dừng ở đây. Với mong ước mỗi bài viết sẽ giúp bạn hiểu và vận dụng thành thạo công thức nên nếu còn vướng mắc hay góp ý hãy để lại và Toanhoc. org sẽ giúp bạn xử lý .

Source: https://thevesta.vn
Category: Bản Tin